최소 공통 조상
이진 트리(Binary Tree)에서 최소 공통 조상(Lowest Common Ancestor)이란,
서로 다른 두 노드의 조상 노드 집합을 각각 A와 B라고 할 때,
교집합(A n B)에 속하는 원소 중 가장 하위에 존재하는 노드를 의미합니다.
여기서 조상 노드 집합이라는 개념은, 본 노드를 포함하는 개념임을 주의해야 합니다.
예를 들어서 A 노드의 조상 노드 집합에는,
A노드보다 상위에 직 / 간접적으로 연결되어 있는 노드 뿐 아니라, A 노드도 포함이 됩니다.

위 이진 트리(Binary Tree)에서 A노드와 B노드의 최소 공통 조상을 찾아보겠습니다.
A와 B의 공통 조상은 핑크색으로 표시해 두었습니다. 이 핑크색으로 표시된 노드 중 가장 하위에 존재하는 노드인 5가 바로 A와 B의 최소 공통 조상(Lowest Common Ancestor)입니다.
우리의 목표는, 이진트리에서 두 노드가 주어졌을 때에 이 두 노드의 최소 공통 조상(LCA)을 찾는 것입니다. 그렇다면 이 LCA를 어떻게 하면 찾을 수 있을까요? 그 방법을 알아보기 전에, 최소 공통 조상에 해당하는 노드가 어떠한 특성을 가지고 있는 지 알아보겠습니다.
최소 공통 조상의 특징
우리는 다음 주어진 이진 트리에서 A와 B의 최소 공통 조상을 구하고 싶습니다.
일단 두 대상 노드 A와 B로부터 루트 방향으로 올라오는 경로를 그려 보겠습니다.
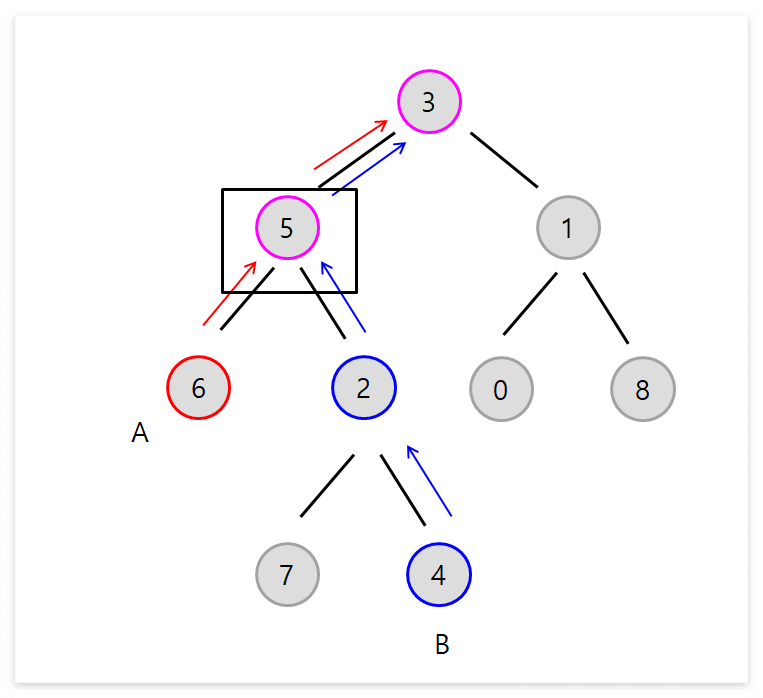
최소 공통 조상인 노드 5번을 보면, 다른 노드와 구별되는 뚜렷한 특징이 존재합니다.
'자손으로부터 올라오는 두 개의 화살표를 모두 가지고 있다'
최소 공통 조상이 되는 노드는, A 노드로부터 루트 노드까지의 경로와 B노드로부터 루트 노드까지의 경로가 최초로 합류하는 지점이기 때문에 위와 같은 특징이 나타나게 되는 것입니다.
"A와 B 노드의 최소 공통 조상(LCA)노드는,
A 노드로부터 루트노드까지의 경로와,
B 노드로부터 루트노드까지의 경로가 최초로 합쳐지는 지점이다.
그래서 두 개의 화살표를 모두 가지게 된다."
그래서 위와 같은 경우는 5번 노드를 반환하도록 코딩이 되어야 할 것입니다.
그런데 반드시 위와 같은 경우만 있는 것은 아닙니다.
다음과 같은 경우도 존재하기 때문입니다.

위 경우 A와 B의 최소 공통 조상 노드는 5번 노드입니다. 이처럼 한 노드의 서브트리 내에 다른 대상 노드가 포함되어서 존재하는 경우에는 처음 본 경우처럼 두 개의 화살표가 동시에 존재하는 그림이 아닙니다.
위와 같은 경우에서는 5 노드를 반환하도록 프로그래밍 해야 합니다.
최소 공통 조상 노드 구하는 코드
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 두 대상 노드로부터 루트노드 방향으로 타고 올라오는 형태가 되게 하기 위하여
// 대상 노드 탐색시, 대상 노드값을 반환하도록 구현
if(root == null || root == p || root == q)
return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 만약 왼쪽 방향 화살표와 오른 쪽 방향 화살표가 모두 존재한다면
// 해당 노드가 최소 공통 조상 노드이므로 반환한다.
if(left != null && right != null)
return root;
else if (right == null)
return left;
else
return right;
}
}
'Algorithm[Java] > Tree' 카테고리의 다른 글
| 이진트리의 직경을 구해보자! [Java / LeetCode 543] (0) | 2024.01.22 |
|---|---|
| BFS를 이용해 이진 트리의 최대 깊이를 구해보자 [Java] (0) | 2024.01.20 |
| DFS를 이용해 이진 트리의 최대 깊이를 구해보자 [Java] (0) | 2024.01.20 |


