URL : https://leetcode.com/problems/maximum-depth-of-binary-tree/description/
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
이진트리가 주어졌을 때에, 이진트리의 최대 깊이를 구하는 문제입니다. 이진트리의 최대 깊이는 DFS(Depth First Search), BFS(Breath First Search) 두 가지 방법을 통해 구할 수가 있는데, 지난 포스팅을 통해 이진트리가 무엇인지, 이진트리의 깊이란 무엇을 말하는 것이며, 이진트리의 깊이를 DFS를 통해 계산하는 알고리즘을 공부한 바 있습니다. 혹여나 관련 개념이 궁금하신 분께서는 다음 포스팅을 참조 부탁 드립니다~
https://akira6036.tistory.com/44
DFS를 이용해 이진 트리의 최대 깊이를 구해보자 [Java]
URL : https://leetcode.com/problems/maximum-depth-of-binary-tree/description/ LeetCode - The World's Leading Online Programming Learning Platform Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get pr
akira6036.tistory.com
오늘은 Depth First Search가 아닌, Breadth First Search(BFS)를 통해서 이진트리의 깊이를 계산하는 알고리즘을 공부해보겠습니다. 본론으로 들어가기 전에, 너비 우선 탐색(Breadth First Search)에 대해 잠시 알아보도록 하죠!
BFS (Breadth First Search) 너비 우선 탐색
너비우선탐색을 정의하기 이전에, 탐색(Search)이라는 것이 과연 무엇인지 알아봅시다. 탐색이라는 것은 다음과 같이 이해하셔도 무방합니다.
"탐색(Search)이란, 특정 노드와 직접 혹은 간접적으로 연결되어 있는 노드들을 모두 방문하는 행위이다"
그렇습니다. 어떠한 그래프가 주어진 상태에서, 노드 A로부터 탐색을 진행한다는 것은, A와 직/간접적으로 연결된 모든 노드들을 모두 방문한다는 의미입니다. 직/간접적으로 연결된 모든 노드들을 방문하는 방법은 여러가지가 있을 수 있겠죠? 바다에서 실종된 조난자를 찾을 때, 'ㄹ'자로 수색을 할 수도 있고, 'ㅁ'자로 수색을 할 수 있듯이 말이죠.
너비우선 탐색은, 다음과 같이 그래프와 탐색 시작점이 주어져 있을 때, 그림과 같은 순서로 방문하는 탐색법을 의미합니다.

탐색 순서는 시작점 노드를 먼저 방문한 후(살구색 노드),
시작점 노드와 가장 가까운 거리에 있는 노드들(파란색 노드),
시작점 노드와 두 번째로 가까운 거리에 있는 노드들(노란색 노드),
시작점 노드와 세 번째로 가까운 거리에 있는 노드들(빨간색 노드)을 방문
...
위와 같은 방식으로 노드 A와 직/간접적으로 연결된 모든 노드를 방문하는 것이 바로 BFS 탐색 방법 입니다. 이걸 가지고 이진트리의 깊이를 어떻게 알 수 있는냐! 이제 그 중요한 이야기를 해 보도록 합시다.
이진트리에서의 너비우선 탐색
그래프에서 너비우선탐색을 한 것과 같이, 이번에는 이진트리에서 너비우선탐색을 적용해 봅시다.

이진트리에서는 루트노드로부터 너비우선탐색을 진행했을 시에, 위와 같은 순서로 방문이 됩니다. 역시 탐색을 시작한 지점으로부터 가장 가까운 곳을 시작으로 먼곳까지 순차적으로 탐색을 해 나갑니다.
첫 번째 턴에서는 탐색 시작점,
두 번째 턴에서는 탐색 시작점과 1의 거리만큼 떨어진 노드들,
세 번째 턴에서는 탐색 시작점과 2의 거리만큼 떨어진 노드들,
네 번째 턴에서는 탐색 시작점과 3의 거리만큼 떨어진 노드들,
규칙이 보입니다! 이진트리의 루트노드에서 BFS를 통한 탐색을 진행해 나가다가, 몇 번째 턴에서 이진트리의 탐색이 완료되는 지를 구하면, 그것이 바로 이진트리의 최대 깊이가 되는 것입니다.
"이진 트리(Binary Tree)의 최대 깊이 = BFS를 통해 루트노드부터 탐색을 하면 몇 번째 턴에 탐색이 완료되는가!"
소스코드 구현
일단, 트리 노드 클래스는 문제에서 다음과 같이 구현이 되어있다고 설명이 되있네요.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
BFS는 큐를 통해 구현합니다.
class Solution {
public int maxDepth(TreeNode root) {
// 만약 null값이 입력되었을 경우 최대깊이 = 0이 된다.
if (root == null)
return 0;
// Linked List 기반의 Queue 선언 및 초기화
Queue<TreeNode> queue = new LinkedList<>();
// 현재까지 탐색된 트리의 깊이. 탐색하면서 갱신해 나갈 예정입니다.
int depth = 0;
// 첫 방문 지점(루트 노드)을 큐에 삽입
queue.offer(root);
...
}
}
위와 같이 연결리스트 기반의 큐를 선언합니다. 참고로, 컬렉션 프레임워크에서 Queue는 인터페이스이고, 이 인터페이스를 구현한 구현체가 바로 LinkedList입니다.
class Solution {
public int maxDepth(TreeNode root) {
...
// Queue가 빌 때까지 탐색을 진행한다
// Queue가 빈다는 것은 이진트리의 탐색이 완료되었다는 의미이다.
while(!queue.isEmpty()) {
// 탐색 깊이 갱신
depth += 1;
// 현재 Queue에 삽입되어있는 노드의 개수 : 아래에서 설명합니다!
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
}
}
return depth;
}
}
어떠한 과정인지 설명하겠습니다.
먼저, 다음 그림과 같이 루트노드를 Queue에 먼저 삽입해서 BFS탐색을 진행할 준비를 하죠.

현재 큐에 A라는 노드가 있는 상태입니다. 이 상태에서 다음의 연산을 진행하면 어떻게 될까요?
// 현재 Queue에 삽입되어있는 노드의 개수
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
위 코드를 실행하면 다음과 같이,
현재 Queue에 삽입되어 있는 노드인 A의 자식노드들이 차례대로 Queue에 삽입되게 됩니다.

현재 큐에 B, C라는 노드가 있는 상태입니다. 이 상태에서 다음의 연산을 진행하면 어떻게 될까요?
// 현재 Queue에 삽입되어있는 노드의 개수
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);위 코드를 실행하면 다음과 같이,
현재 Queue에 삽입되어 있는 노드인 B, C의 자식노드들이 차례대로 Queue에 삽입되게 됩니다.

현재 큐에 D,E,F 라는 노드가 있는 상태입니다. 이 상태에서 다음의 연산을 진행하면 어떻게 될까요?
// 현재 Queue에 삽입되어있는 노드의 개수
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
위 코드를 실행하면 다음과 같이,
현재 Queue에 삽입되어 있는 노드인 D, E, F의 자식노드들이 차례대로 Queue에 삽입되게 됩니다.
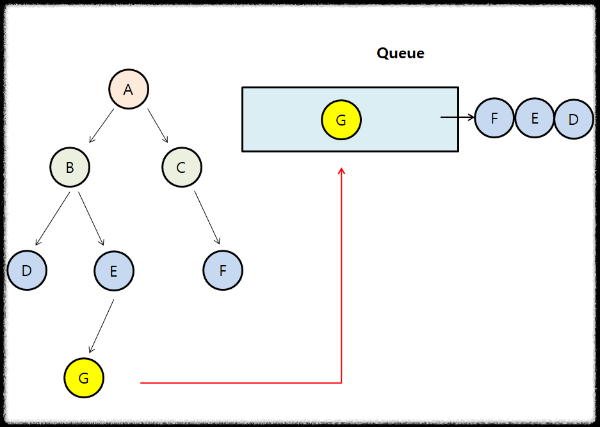
현재 큐에 G 라는 노드가 있는 상태입니다. 이 상태에서 또 동일한 연산을 진행하면 어떻게 될까요?
// 현재 Queue에 삽입되어있는 노드의 개수
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
위 코드를 실행하면 다음과 같이,
현재 Queue에 삽입되어 있는 노드인 G의 자식노드들이 차례대로 Queue에 삽입되게 되는데, G의 자식노드가 없으므로, Queue가 비게 됩니다. Queue가 비기 때문에, 다음 반복문을 빠져나와서, 최종 이진트리의 깊이가 반환되는 것이죠.

앞서 우리가 반복해서 진행했던 연산 기억 나시죠?
// 현재 Queue에 삽입되어있는 노드의 개수
int q_size = queue.size();
// 현재 Queue에 삽입되어있는 노드들의 자식노드를 Queue에 삽입한다.
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
이 연산이 총 얼마만큼 반복되었는가를 세기만 한다면, 이진트리의 최대 깊이를 구할 수 있는 것입니다.
전체 소스코드
class Solution {
public int maxDepth(TreeNode root) {
if (root == null)
return 0;
Queue<TreeNode> queue = new LinkedList<>();
int depth = 0;
queue.offer(root);
while(!queue.isEmpty()) {
depth += 1;
int q_size = queue.size();
for(int i=0; i < q_size; i++) {
TreeNode node = queue.poll();
if(node.left != null)
queue.offer(node.left);
if(node.right != null)
queue.offer(node.right);
}
}
return depth;
}
}'Algorithm[Java] > Tree' 카테고리의 다른 글
| Lowest Common Ancestor of a Binary Tree 최소 공통 조상 알고리즘 [LeetCode 236] (0) | 2024.04.01 |
|---|---|
| 이진트리의 직경을 구해보자! [Java / LeetCode 543] (0) | 2024.01.22 |
| DFS를 이용해 이진 트리의 최대 깊이를 구해보자 [Java] (1) | 2024.01.20 |


