URL : https://leetcode.com/problems/maximum-depth-of-binary-tree/description/
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
이진트리가 주어졌을 때에, 이진트리의 최대 깊이를 구하는 문제입니다. 이진트리의 최대 깊이는 DFS(Depth First Search), BFS(Breath First Search) 두 가지 방법을 통해 구할 수가 있는데, 어떻게 최대 깊이를 구하는가에 앞서서, 이진트리가 무엇인지, 그리고 이진트리의 최대 깊이가 무엇인지를 살펴보고 가도록 하겠습니다. 개념은 언제나 중요하니까요!
이진트리(Binary Tree)란 무엇인가요?
간단하게 다음과 같이 알아두셔도 괜찮습니다.
"트리의 모든 구성원 노드가 최대 두 개의 자식 노드를 가질 때, 우리는 그 트리를 이진트리라고 부른다"
어떠한 트리가 이진트리가 되려면, 그 트리를 구성하는 전체 노드가 최대 두 개의 자식노드를 가져야 합니다. 트리에 속해있는 어떠한 노드라도 3개 이상의 자식노드를 가진다면, 그 트리는 이진트리가 아니게 되는 것이죠! 정리해볼까요? 트리에 속해있는 모든 노드가 다음 조건을 만족해야 하는 것입니다.
- 자식노드를 가지지 않는다
- 하나의 자식노드를 가진다
- 두 개의 자식노드를 가진다

위 그림에서, 좌측의 트리는 이진트리입니다. 왜냐하면 좌측의 트리를 구성하는 모든 노드가 위 세 가지 조건을 만족하기 때문이죠. 그러나 우측의 트리는 이진트리가 아닙니다. 왜냐하면 우측의 트리를 구성하는 노드 중, 빨간색으로 색칠된 노드가 3개의 자식 노드를 가지고 있기 때문입니다.
간단하게 이진트리의 개념을 알아보았습니다.
이진트리(Binary Tree)의 깊이란 무엇인가요?
사실 이진트리의 깊이라는 개념은 논문이나 문서마다 다르게 정의합니다ㅠㅜ 원래 트리의 깊이(Depth of Tree)라는 것은 루트 노드로부터 모든 노드까지 도달하는 데 최대 얼마만큼의 비용이 소요되는가를 의미하지만, 이 문제에서는 이진트리의 깊이를 다음과 같이 정의하고 있네요!
"A binary tree's maximum depth is the number of nodes
along the longest path from the root node down to the farthest leaf node."
즉, 다음과 같은 트리에서는 루트노드로부터 가장 먼 노드까지 가는 데 경유하는 노드가 총 4개이니, 이진트리의 깊이는 총 4개가 되는 것입니다.

이상 이진트리와 이진트리의 깊이에 대해서 알아보았으니, 이진트리가 주어졌을 때 얼마만큼의 깊이를 가지게 되는가를 계산하는 알고리즘을 공부해 보도록 하겠습니다!
이진트리(Binary Tree)의 깊이를 구하는 방법 : DFS 깊이 우선 탐색법
어떤 노드가 주어졌을 때, 그 노드의 최대 깊이는 얼마일까요?
답은 매우 간단합니다. 특정 노드의 최대 깊이는 다음과 같이 구할 수가 있습니다.
어떤 노드의 최대 깊이 = 왼쪽 자식노드의 최대 깊이 + 오른쪽 자식노드의 최대 깊이
진짜로 그런지 확인을 해 볼까요?
첫 번째 예시
다음 그림에서 파란색 노드의 최대 깊이를 구해 봅시다.

파란색 노드의 좌측 자식노드의 최대깊이는 1(연두색 노드 개수)
파란색 노드의 우측 자식노드의 최대깊이는 2(살구색 노드 개수) 입니다.
이러한 상황에서 파란색 노드의 최대 깊이는 1(좌측 자식노드의 최대깊이)과 2(우측 자식노드의 최대깊이)중 더 큰 값인 2에다가 1을 더한 것이 되는 것입니다.
두 번째 예시
다음 그림에서 파란색 노드의 최대 깊이를 구해 봅시다.

파란색 노드의 좌측 자식노드의 최대깊이는 3(살구색 노드 개수)
파란색 노드의 우측 자식노드의 최대깊이는 2(연두색 노드 개수) 입니다.
이러한 상황에서 파란색 노드의 최대 깊이는 3(좌측 자식노드의 최대깊이)과 2(우측 자식노드의 최대깊이)중 더 큰 값인 3에다가 1을 더한 것이 되는 것입니다.
재귀적 구조 발견
특정 노드의 최대깊이를 구하는 식을 다시 상기시켜 볼까요?
어떤 노드의 최대 깊이 = 왼쪽 자식노드의 최대 깊이 + 오른쪽 자식노드의 최대 깊이
재귀적 구조에 익숙하신 분들이라면 벌써 눈치를 채셨는지 모르겠습니다! 어떤 노드의 최대깊이(좌측 파란색 볼드체)를 정의할 때, 해당 자식노드들의 최대깊이(우측 빨간색 볼드체)가 사용이 됩니다. 어떠한 함수의 정의에서 해당 함수가 동일하게 사용되는 것, 이것은 전형적인 재귀(Recurssion) 구조입니다.
그래서 특정 노드가 전달되었을 때 해당 노드의 최대깊이를 구하는 함수는 다음과 같이 정의되어야 합니다.
class Solution {
public int maxDepth(TreeNode root) {
...
int left = maxDepth(root.left); // 왼쪽 자식노드의 최대 깊이
int right = maxDepth(root.right); // 오른 쪽 자식노드의 최대 깊이
// 본 노드의 최대 깊이 = (좌/우측 자식노드의 최대깊이중 큰 것) + 1
return Math.max(left, right) + 1;
}
}
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
그런데 이렇게만 정의하면 끝날까요? 재귀구조를 통해 로직을 세울때는 반드시 종료조건을 명시해야됩니다.
다음과 같은 상황을 예로 들어볼까요?
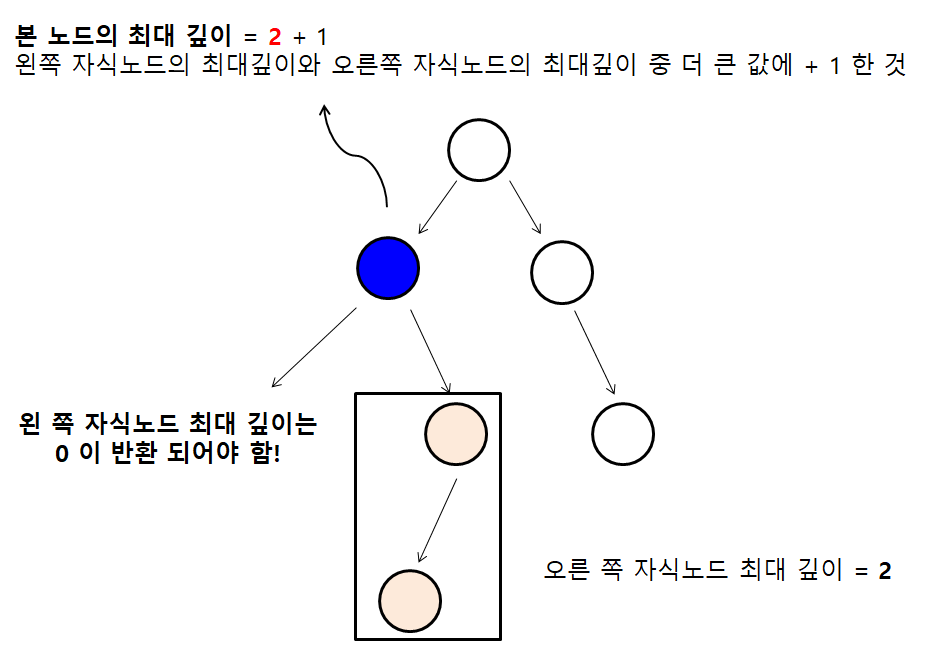
우리는 파란색 노드의 최대깊이를 구할 때에 왼쪽 자식노드와 오른쪽 자식노드의 최대깊이를 구해야 합니다. 우측 자식노드는 있지만, 좌측 자식노드는 존재하지 않는 상황입니다. 좌측 자식노드가 존재하지 않다면 해당 측의 최대 깊이 값이 0이 나오도록 구현을 해야 올바르게 노드의 최대깊이를 구할 수가 있을 것입니다.
그래서 maxDepth라는 재귀함수의 앞부분에 다음과 같은 코드를 추가해주면 됩니다.
class Solution {
public int maxDepth(TreeNode root) {
// 존재하지 않는 자식노드에서 호출이 된다면 0을 반환
if (root == null)
return 0;
int left = maxDepth(root.left);
...
}
}
전체 소스코드
전체 소스코드는 다음과 같습니다.
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
// 존재하지 않는 자식노드에서 호출이 된다면 0을 반환
if (root == null)
return 0;
int left = maxDepth(root.left); // 좌측 자식노드의 최대깊이
int right = maxDepth(root.right); // 우측 자식노드의 최대깊이
// 본 노드의 최대 깊이 = (좌/우측 자식노드의 최대깊이중 큰 것) + 1
return Math.max(left, right) + 1;
}
}'Algorithm[Java] > Tree' 카테고리의 다른 글
| Lowest Common Ancestor of a Binary Tree 최소 공통 조상 알고리즘 [LeetCode 236] (0) | 2024.04.01 |
|---|---|
| 이진트리의 직경을 구해보자! [Java / LeetCode 543] (0) | 2024.01.22 |
| BFS를 이용해 이진 트리의 최대 깊이를 구해보자 [Java] (0) | 2024.01.20 |


