[슈바르츠 부등식] 벡터의 내적을 이용한 Schwarz Inequality 증명하기

오늘은 벡터의 내적을 이용하여 슈바르츠 부등식을 증명해 보도록 하겠습니다.

먼저 Schwarz Inequality의 원형은 다음과 같습니다.

 

A벡터와 B벡터가 있다고 가정할 때,

A와 B의 내적값에 절댓값을 씌우면,

그 값은 A벡터의 크기 * B벡터의 크기보다 작거나 같습니다.

 

 

증명하기

먼저 B벡터가 영벡터(Zero Vector)이면 명제가 참 입니다.

 

B벡터가 영벡터가 아닐 경우를 살펴 보겠습니다.

 

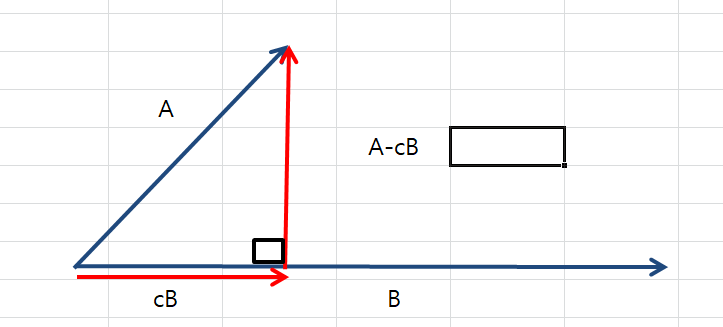
A벡터와 B벡터가 위 그림가 같다고 해 봅시다.

그리고 B와 방향이 같은 cB벡터는

A벡터를 B벡터로 투영시킨 Projected Vector 입니다.

 

위 그림에서

피타고라스 정리에 의해 다음 식이 성립합니다.

A벡터의 길이를 ||A||이라고 하면

 

||A|| ^ 2 = ||cB|| ^ 2 + || A - cB ||^2

 

위 식에서 다음 부등식 성립합니다.

 

||cB|| ^ 2 <= ||A||^2

 

이를 전개하면 다음과 같이 됩니다.

(A가 B에 투영된 투영벡터에서 c가 A.B / B.B로 어떻게 변환되는지는 나중에 설명 드리겠습니다.)

따라서 최종적으로 다음과 같이 되고.

 

이를 또 정리하면

|A.B|^2 <= || A || ^ 2 * || B || ^ 2가 됩니다.

따라서, |A.B| <= || A || * || B ||가 성립하게 되는 것입니다.

 

 

# 투영벡터의 cB에서 c가 A.B / A.A가 되는 이유

 

이 그림에서

피타고라스 정리에 의하여

|| A || ^ 2 = || cB || ^2 + || A - cB || ^2가 됩니다.

이걸 전개하면 위 식처럼 c값이 나오는 것을 알 수가 있습니다.

 

 

이건 하나의 공식처럼 외워두는 것을 추천 드립니다.

A벡터를 B벡터로 투영시킨 Projected Vector는

((A.B) / (B.B)) * B