안녕하세요, 오늘은 오름차순으로 정렬된 배열이 주어져 있을 때에,
이 배열에서 특정 값의 Lower Bound와 Upper Bound를 어떻게 찾을 수 있는가에 대해서 설명을 드리도록 하겠습니다.
먼저 Lower Bound와 Upper Bound가 무엇인지 설명을 드리도록 하겠습니다.
Lower Bound와 Upper Bound
"오름차순으로 정렬되어 있는 배열에서, 특정 값 보다 크거나 같은 값을 가지는 최소 인덱스를 바로 Lower Bound(하한)이라고 합니다.
이해하기 쉽게 그림으로 나타내자면 다음과 같습니다.

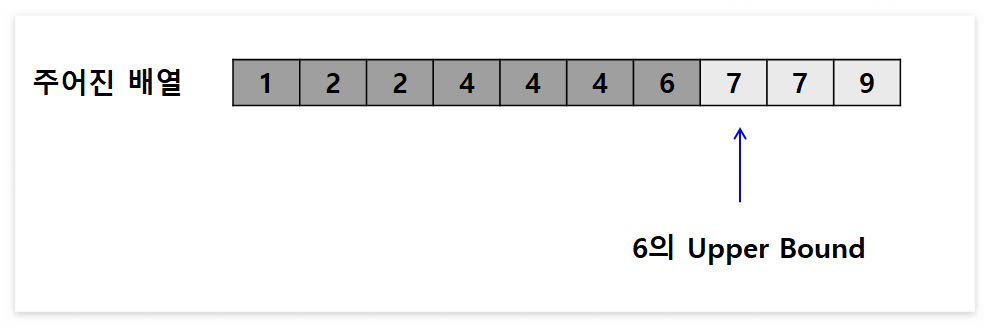
위 그림에서 오름차순으로 주어진 배열에 대하여, 6의 Lower Bound는 파란색의 화살표가 가리키는 곳이 됩니다.
위 배열에서 진하게 회색으로 색칠되어 있는 곳은 모두 6과 같거나 작은 값이며,
연한 회색으로 색칠되어 있는 곳은 모두 6보다 큰 값입니다.
그리고 "오름차순으로 정렬되어 있는 배열에서, 특정 값 보다 큰 값을 가지는 최소 인덱스를 바로 Upper Bound(상한)이라고 합니다.
이해하기 쉽게 그림으로 나타내자면 다음과 같습니다.
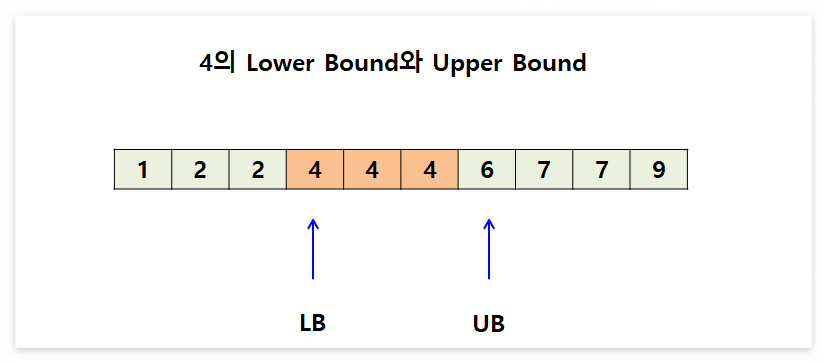
더 쉽게 파악하기 위해 다른 예시를 들어보겠습니다. 이번 예시를 보시면 더욱 Lower Bound와 Upper Bound가 어떠한 의미인지 정확하게 와 닿으실 것입니다.

오름차순으로 정렬된 배열에서 4라는 값의 Lower Bound와 Upper Bound를 찾아보았습니다. 즉, Lower Bound 이상과 Upper Bound미만에 해당하는 인덱스에 우리가 찾는 target값이 존재하게 되는 것입니다.
다음 예시들을 통해 추가적으로 Lower Bound와 Upper Bound를 찾는 것을 연습해보겠습니다.


어디다가 써먹는가?
Lower Bound와 Upper Bound를 공부할 때 이걸 왜 사용하는지에 대한 확신이 오지 않으면, 사실 시간내서 공부할 마음을 잡기가 쉽지 않습니다. 이 Lower / Upper Bound를 사용하면 다음과 같은 작업을 매우매우 빠르게 진행해낼 수가 있습니다.
먼저, 전 지구상의 70억명 사람들이 키 순서대로 일렬로 나란하게 서 있다고 가정을 해 보겠습니다. 그리고 우리는 다음과 같은 사실을 알고 싶습니다.
키가 140cm 이상인 조건을 최초로 만족하는 사람이 몇 번째에 존재하는가?
키가 170cm보다 작은 사람은 처음부터 몇 번째까지 존재하는가?
위 문제의 해답은, Lower Bound / Upper Bound를 찾는 알고리즘을 이용해서 O(log2n)의 시간복잡도에 구할 수 있습니다. 만약 이 lower bound 알고리즘을 사용하지 않고 처음부터 끝까지 모든 사람들을 탐색해서 찾는다면 O(n)의 시간복잡도가 소요됩니다. 여기서 제한된 조건은 '키'이기 때문에 70억명의 모든 인구를 탐색하는 일은 발생하지 않겠지만, 그걸 유념하더라도 O(log2n)의 시간복잡도에 비하여 문제 해결 시간이 압도적으로 많이 걸리는 것은 사실입니다.
Lower Bound를 구하는 방법
우선 다음과 같은 배열이 주어져 있다고 해 보겠습니다.
그리고 이 배열에서 8이라는 값의 Lower Bound를 찾아보도록 하겠습니다.
Lower Bound나 Upper Bound나 찾는 원리는 똑같습니다.
"Lower Bound 혹은 Upper Bound가 될 수 있는 후보군들의 범위를 이진탐색(Binary Search)을 통해 좁혀 나간다"
"범위를 좁혀 나가다가 딱 하나의 후보군만이 남을 경우, 그 후보군이 바로 Lower Bound혹은 Upper Bound이다."

우리의 목표는 그림에 나와 있듯이, 8보다 높거나 같은 값의 원소를 가지는 최소 인덱스를 찾는 것입니다. 그렇다면, 어떠한 인덱스들이 후보군이 될 수 있을까요? 바로, 다음 그림에서 핑크색으로 표시된 인덱스들 입니다. 처음에는 당연히 아무런 정보도 주어져 있지 않으니까, 모든 인덱스들을 그 후보군의 대상에 올려놓는 것입니다.

위와 같은 조건에서 시작을 해서, 아까 말씀드린 대로, 이진 탐색을 해서 점점 그 후보군들을 좁혀 나갈 것입니다. 이렇게 좁혀 나가다가 단 하나의 후보군 인덱스가 남으면, 그 인덱스가 바로 Lower Bound입니다.
그런데 조금 이상한 것이 있습니다. 배열은 크기가 8이고 맨 마지막 인덱스는 분명 7인데, 왜 7보다 하나 더 큰 8번째 인덱스까지 후보군에 넣는 것일까요? 이것은 바로 다음의 경우를 고려한 것이랍니다.
"배열의 모든 인덱스가 8보다 작은 경우,
8보다 같거나 큰 값을 가지는 최소 인덱스는 배열의 마지막 인덱스 + 1 이다"
자, 이제 본격적으로 정답이 될 수 있는 후보군들을 좁혀 나가보도록 하겠습니다.
우리가 아까 인덱스의 후보군을 줄여나갈 때 이진 탐색(Binary Search)이라는 알고리즘을 이용한다고 말씀드린 바 있습니다.

가장 먼저, 현재 후보군 인덱스의 가장 왼쪽을 Left, 가장 오른쪽 인덱스를 Right라고 하고, 그 중간 인덱스인 Middle의 값을 확인해 보겠습니다. 이 Middle이라는 값을 확인해 보니 7이네요.
그러면 이 middle을 포함한 이하의 모든 원소들은, "8보다 같거나 큰 값을 가지는 최소 인덱스"의 후보군이 될 수가 없습니다. 왜냐하면 middle을 포함해서 그 이하의 모든 원소들은 8보다 작은 값이기 때문입니다. 그래서 위와 같이 후보군이 정리가 되는 것입니다.

또 위와 같은 과정을 반복합니다. 현재 시점에서의 후보군 가장 왼 쪽의 인덱스를 Left, 가장 오른 쪽의 인덱스를 Right라고 해 보겠습니다. 그리고 그 중간 인덱스인 6번 인덱스 값을 보니 11이라는 값입니다. 그리고 이는 우리가 타겟으로 하는 8보다 큰 값입니다.
우리가 찾는 것은 8의 Lower Bound, 즉 "8보다 같거나 큰 값을 가지는 최소 인덱스"를 찾는 것입니다. 그러면 위와 같은 결과가 나왔을 때에 후보군 범위를 어떻게 조정할 수가 있을까요? 6번 인덱스 값이 11로, 8보다 큰 값을 가집니다. 그러면 6번 인덱스보다 큰 7번과 8번,.. 인덱스들은 우리가 찾는 인덱스의 후보군이 절대로 될 수가 없습니다.
그래서 우리가 찾는 인덱스의 후보군을 위와 같이 줄일 수가 있는 것입니다. 소스코드를 이해하는 것보다, 이렇게 후보군들을 점차적으로 이진탐색을 통해 좁혀 나간다는 개념을 이해하는 것이 더 중요합니다. 이렇게 후보군들을 줄여나가는 규칙을 파악하면 Lower bound나 후에 기재할 Upper bound알고리즘이나 그 코드를 구현하는 것은 시간문제입니다.

또 같은 과정을 반복합니다. 후보군 인덱스의 가장 왼쪽과 가장 오른쪽의 중간 인덱스를 조사합니다. 그 5번 인덱스의 값이 9로, 우리가 관심 있는 대상인 8보다 더 큰 숫자입니다. 그렇다면 역시, 이 5번 인덱스 이후의 5번 6번 7번...인덱스들은 모두, 우리가 찾는 인덱스의 후보군이 될 수가 없습니다.
결국 이렇게 이진 탐색을 반복하다가 보면 단 하나의 후보군이 남게 되고, 이 인덱스가 바로 우리가 찾고자 하는 Lower Bound 인덱스가 되는 것입니다.
8보다 크거나 같은 값을 가지는 최소 인덱스는 바로 5번 인덱스입니다.
소스코드로 구현하면 다음과 같습니다.
다음 코드에서 left < right로 반복문의 조건을 설정하는 이유는, 후보군 인덱스가 단 하나 남았을 때 이 인덱스를 정답으로 리턴하기 위함입니다.
def lower_bound(arr, left, right, k):
while left < right:
mid = (left + right)//2
if arr[mid] < k:
left = mid + 1
else:
right = mid
return right
다시 말씀드리자면, 매 단계마다 가운데 값을 찾고, 이 가운데 값을 기반으로 후보군의 범위를 줄여나간다는 개념을 이해하는 것이 가장 우선되어야 하고, 이것만 이해하면 다음 두 가지를 모두 이해할 수 있습니다.
- 특정 값보다 크거나 같은 값을 가지는 최소 인덱스 찾기 (Lower Bound)
- 특정 값보다 큰 값을 가지는 최소 인덱스 찾기(Upper Bound)
Upper Bound
Upper Bound의 소스코드는 다음과 같습니다. 우리가 찾는 것은 특정 값(target)보다 큰 값을 가지는 최초의 인덱스를 구하는 것입니다. 이를 이분탐색을 이용해서, 즉 Lower Bound와 같은 비슷한 과정을 거쳐 구하게 되면 다음과 같이 코드로 나타낼 수 있습니다.
public static int getUpperBound(int[] arr, int target) {
int l = 0;
int r = arr.length;
while(l < r) {
int mid = l + (r-l) / 2;
int midValue = arr[mid];
if(midValue > target)
r = mid;
else
l = mid+1;
}
return l;
}