URL : https://leetcode.com/problems/keys-and-rooms/description/
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
오늘은 전형적인 그래프 탐색 문제, Keys and Rooms문제를 풀어보도록 하겠습니다. 제가 알고리즘을 공부했던 초창기에 이런 문제들을 접하면서 많이 놀랐던 기억이 납니다ㅎㅎ
그래프면 노드(node)랑 엣지(edge)가 나와야 되는거 아니야? 이게 그래프 문제라고?
하면서요. 그런데 점점 많은 그래프 문제들을 접하면서 그러한 선입견을 깨게 되었습니다. 모든 경우를 달성할 수 있는 지 여부를 판단하는 문제, 가장 좋은 경우를 찾는 문제 등등 탐색의 과정이 필요한 모든 상황이 그래프로 모델링이 가능하며, 이렇게 상황을 그래프로 모델링해서 풀어낼 수 있는 모든 문제를 그래프 알고리즘 문제라고 부릅니다.
문제 상황 이해
먼저 문제를 읽어보도록 하겠습니다.
There are n rooms labeled from 0 to n - 1 and all the rooms are locked except for room 0. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of distinct keys in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array rooms where rooms[i] is the set of keys that you can obtain if you visited room i, return true if you can visit all the rooms, or false otherwise.
Example 1:
Input: rooms = [[1],[2],[3],[]]
Output: true
Explanation:
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.
Example 2:
Input: rooms = [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can not enter room number 2 since the only key that unlocks it is in that room.
Constraints:
- n == rooms.length
- 2 <= n <= 1000
- 0 <= rooms[i].length <= 1000
- 1 <= sum(rooms[i].length) <= 3000
- 0 <= rooms[i][j] < n
- All the values of rooms[i] are unique.
결국 우리가 풀어내야 하는 것은 다음을 확인하는 것입니다.
0번 방부터 방문을 하기 시작하여, 주어진 모든 방을 방문할 수 있는 가?
시작할 때 0번 방을 제외한 다른 모든 방은 잠겨져 있는 상태입니다.
각 방에는 열쇠(key)가 들어있는데, 이 열쇠로 잠겨진 방문을 열어낼 수가 있습니다.
우리는 어떤 방을 방문할 때마다, 방문한 방에 들어있는 모든 열쇠를 가져올 수가 있습니다.
아이디어
이 문제를 그래프로 표현을 해 보자면, 0번 방부터 방문을 시작했을 때에 모든 방에 방문할 수 있는가?를 확인하는 문제입니다.
문제에서 주어진 두 번째 예시를 이용해서 설명을 진행하겠습니다.

문제에서 처음에 rooms = [[1,3], [3,0,1],[2],[0]]으로 주어져 있고,
이는 위 그림처럼 모델링 될 수가 있습니다.
0번 방에는 : 1번 방을 열 수 있는 키, 3번 방을 열 수 있는 키
1번 방에는 : 3번 방을 열 수 있는 키, 0번 방을 열 수 있는 키, 1번 방을 열 수 있는 키
2번 방에는 : 2번 방을 열 수 있는 키
3번 방에는 : 0번 방을 열 수 있는 키
가 존재하는데, 이걸 위 그림처럼 표현할 수 있는 것입니다.
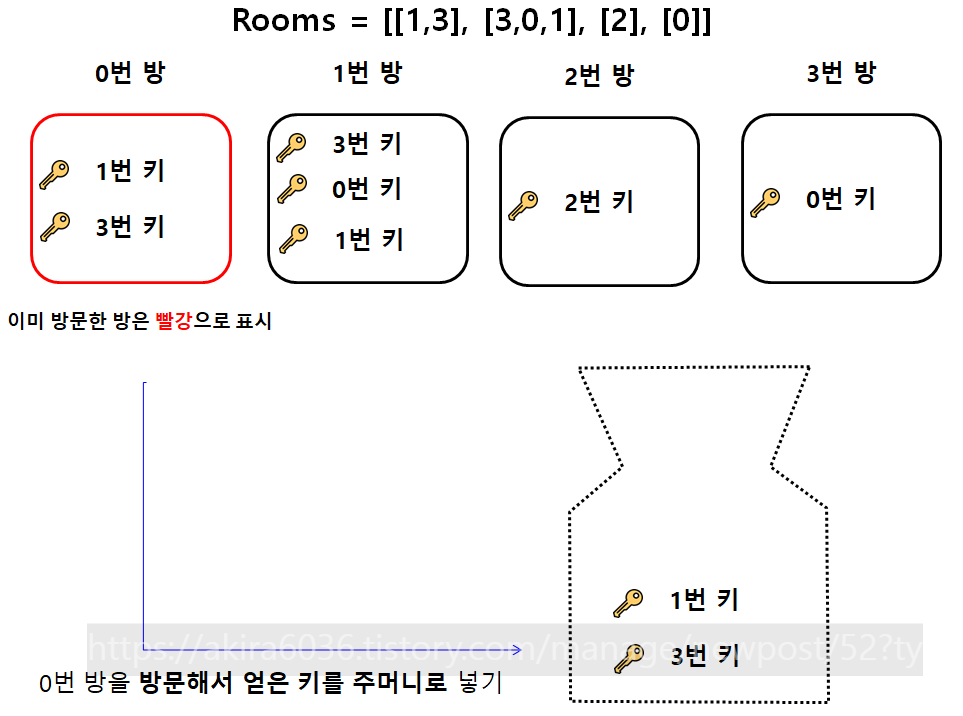
문제에서는 맨 먼저 0번째 방을 방문하라고 합니다.
문제에서 요구한 대로 0번째 방을 방문하고, 0번째 방에 있던 열쇠를 모두 가지고 나옵니다.
우리에게는 키를 담는 열쇠 주머니가 있습니다.
매 단계에서 이 열쇠 주머니에, 방금 방문했던 방에 있는 모든 열쇠들을 집어넣을 것입니다.
0번째 방에 있던 열쇠들을 모두 이 열쇠 주머니에 집어넣습니다.

이제 우리가 할 일은 무엇인가요?
0번 방의 방문이 끝났으니, 다음 방을 방문해야죠.
이처럼, 매 단계에서 방을 나오게 되면, 다음에 어느 방으로 들어갈지를 골라야 합니다.
그러면 다음에 어느 방으로 들어갈 지를 어떻게 고를까요?
우리가 가지고 있는 열쇠 주머니에서 키를 하나 꺼냅니다. 그리고 그 키로 열 수 있는 방을 방문하는 것입니다.
키를 주머니에서 하나 꺼내고, 그 키에 해당하는 방이, 우리가 아직 방문하지 않은 방이라면, 그곳을 들어갑니다.

1번째 방을 방문 후, 해당 방에 있던 모든 열쇠들을 열쇠 주머니에 넣어줍니다.

이제 1번 방의 방문이 끝났으니, 다음 방을 방문해야죠.
키를 주머니에서 하나 꺼내고, 그 키에 해당하는 방이, 우리가 아직 방문하지 않은 방이라면, 그곳을 들어갑니다.

3번째 방을 방문 후, 해당 방에 있던 모든 열쇠들을 열쇠 주머니에 넣어줍니다.

이제 3번 방의 방문이 끝났으니, 다음 방을 방문해야죠.
키를 주머니에서 하나 꺼내고 보니, 0번 방의 키가 나왔습니다.
그런데 0번 방은 우리가 이전에 이미 방문했던 곳이므로, 방문하지 않아도 됩니다.
왜냐하면 그 0번 방은 이미 방문이 완료되었고, 그 방에 있던 모든 열쇠들은 이미 가지고 나왔기 때문입니다.
이처럼, 매 단계에서 열쇠 주머니에서 열쇠를 꺼내면서, 그 열쇠가 우리가 이미 방문했던 방을 여는 열쇠라면
그 열쇠를 버립니다.

역시 0번 방은 이미 방문했던 방이므로 패스

역시 3번 방도 이미 방문했던 방이므로 패스

열쇠주머니에서 정신없이 열쇠를 꺼내다 보니, 열쇠 주머니가 비어서 더이상 열쇠를 꺼낼 수가 없습니다.
이것이 무슨 의미일까요?
열쇠 주머니가 비었다는 것은, 원래 시작점(0번 방)으로 부터 시작을 한 탐색이 완료되었다는 것을 의미합니다. 방문 가능한 모든 지점을 방문했고, 더이상 탐색을 진행할 수 없다는 의미입니다.
이렇게, 탐색이 완료된 시점에서, 내가 방문한 방에 총 몇개인지를 셉니다.(빨간색으로 표시된 방)
방은 총 4개인데, 내가 방문한 방이 3개밖에 없다면
주어진 조건으로는, 0번 방을 시작으로 모든 방의 방문이 불가능하다는 의미입니다.
탐색이 완료된 시점에서, 내가 방문한 방이 전체 방보다 적다면, 시작점을 시작으로 모든 방을 방문할 수 없다는 의미이다.
여기까지 보신 후에 후술할 소스코드를 보시면 더욱 이해가 잘 되실 것이라고 생각합니다.
열쇠 주머니의 비밀
우리가 매 방을 방문할 때마다 열쇠주머니에다가 열쇠를 넣어주고,
다음 방을 어디로 방문할 지 정할 때마다 열쇠주머니로부터 열쇠를 추출하는 과정을 했었습니다.
이 열쇠주머니를 Stack으로 정의한다면 위 과정이 DFS(Depth First Search)를 통한 탐색이 되는 것이고
이 열쇠주머니를 Queue로 정의한다면 위 과정이 BFS(Breadth Firsth Search)를 통한 탐색이 되는 것입니다.
이 글을 읽으시면서 공부하시는 분이라면 DFS와 BFS의 개념은 아실 확률이 높으니 따로 설명하지 않겠습니다.
핵심은,
가장 나중에 주머니에 삽입된 열쇠가 가장 최초로 추출되도록 구현된 열쇠 주머니라면 DFS방식의 탐색
가장 처음에 주머니에 삽입된 열쇠가 가장 최초로 추출되도록 구현된 열쇠 주머니라면 BFS방식의 탐색
이 되는 것입니다.
전체 소스 코드
열쇠 주머니를 Stack으로 정의하였을 경우의 DFS풀이
열쇠 주머니를 Queue로 정의하였을 경우의 BFS풀이를 차례대로 첨부하였습니다.
// DFS
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
// 이미 방문한 지점을 방문하지 않도록 하기 위한 Map생성
Map<Integer, Boolean> visited = new HashMap<>();
// 열쇠주머니
Deque<Integer> stack = new ArrayDeque<>();
// 가장 첫번째 지점인 0번 방을 방문 후,
// 0번 방의 열쇠를 주머니에 집어넣는다
visited.put(0, true);
for(int key : rooms.get(0))
stack.push(key);
// 탐색이 완료될 때까지 반복!
// 주머니가 빈다는 것은 탐색이 완료되었음을 의미한다
while(!stack.isEmpty()) {
// 열쇠 주머니에서 키를 꺼낸다
int key = stack.pop();
// 꺼낸 키가 아직 방문하지 않은 방에 해당하는 키라면
if(!visited.containsKey(key)) {
// 그 지점을 방문하고
visited.put(key, true);
// 그 방에 있던 모든 열쇠를 열쇠 주머니에 넣는다
for(int next : rooms.get(key))
stack.push(next);
}
}
// 방문이 완료되었을 때에 내가 방문한 방이 총 방의 개수보다 적다면 false반환
if(visited.size() < rooms.size())
return false;
else
return true;
}
}
// BFS
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
Map<Integer, Boolean> visited = new HashMap<>();
// Deque<Integer> stack = new ArrayDeque<>();
Queue<Integer> queue = new LinkedList<>();
visited.put(0, true);
for(int key : rooms.get(0)) {
queue.offer(key);
}
while(!queue.isEmpty()) {
int key = queue.poll();
//If not visited!
if(!visited.containsKey(key)) {
visited.put(key, true);
for(int next : rooms.get(key))
queue.offer(next);
}
}
if(visited.size() < rooms.size())
return false;
else
return true;
}
}