Determine if Two Strings Are Close [Java / LeetCode 1657]

URL : https://leetcode.com/problems/determine-if-two-strings-are-close/?envType=study-plan-v2&envId=leetcode-75

LeetCode - The World's Leading Online Programming Learning Platform

 

 오늘은 Hash Table로 분류된 알고리즘 문제, "Determine if Two String Are Close"라는 문제를 풀어보도록 하겠습니다.

 문제 설명

Two strings are considered close if you can attain one from the other using the following operations:

• Operation 1: Swap any two existing characters.
  • For example, abcde -> aecdb
• Operation 2: Transform every occurrence of one existing character into another existing character, and do the same with the other character.
  • For example, aacabb -> bbcbaa (all a's turn into b's, and all b's turn into a's)

You can use the operations on either string as many times as necessary.

Given two strings, word1 and word2, return true if word1 and word2 are close, and false otherwise.

Example 1:
Input: word1 = "abc", word2 = "bca"
Output: true
Explanation: You can attain word2 from word1 in 2 operations.
Apply Operation 1: "abc" -> "acb"
Apply Operation 1: "acb" -> "bca"

 

Example 2:

Input: word1 = "a", word2 = "aa"
Output: false
Explanation: It is impossible to attain word2 from word1, or vice versa, in any number of operations.

Example 3:

Input: word1 = "cabbba", word2 = "abbccc"
Output: true
Explanation: You can attain word2 from word1 in 3 operations.
Apply Operation 1: "cabbba" -> "caabbb"
Apply Operation 2: "caabbb" -> "baaccc"
Apply Operation 2: "baaccc" -> "abbccc"

• Constraints:
• 1 <= word1.length, word2.length <= 105
• word1 and word2 contain only lowercase English letters.

 

 문자열 word1과 word2가 주어졌을 때에, word1에 일련의 operation 1과 operation2라는 연산을 해서, word2로 바꿀 수 있는 가 여부를 판단하는 문제입니다. 

 

 Operation1과 Operation2의 의미

 그러면 operation1과 operation2가 어떤 종류의 연산인지 파악해 보도록 하겠습니다.

일단 operation1이라는 것은, 주어진 문자열 내에 존재하는 임의 두 개의 알파벳 간 위치를 교환하는 연산입니다.

 

문자열 word에 Operation1을 하는 것의 예시를 들어보겠습니다.

 

"aabbc" → "cabba" (빨간색으로 표시된 a와 c 알파벳의 위치 교환)

"abcccdeerfs" → " afcccdeerbs " (빨간색으로 표시된 b와 f알파벳의 위치 교환)

"sfwerf" → "sfewrf" (빨간색으로 표시된 w와 e 알파벳의 위치 교환)

 

 operation2라는 연산은, 주어진 문자열 내에 존재하는 하나의 모든 알파벳을, 문자열 내에 존재하는 다른 알파벳 군(群)과 바꾸는 연산입니다. 예를 들어보도록 하겠습니다.

 

"aabbcffffffff" → "ffbbcaaaaaaaa" (알파벳 a군과 알파벳 f군을 서로 교환)

"aaaaaaaaaaaaabbbc" → "cccccccccccccbbba" (알파벳 a군과 알파벳 c군을 서로 교환)

"bbccdef" → "eeccdbf" (알파벳 b군과 알파벳 e군을 서로 교환)

 

 

 주어진 두 문자열의 개수가 다른 경우

 갑자기 "서로"라는 단어가 나오는데, 서로 라는 것은 주어진 word1과 word2라는 문자열을 의미하는 것입니다. (우리의 목적은 word1에 operation1과 operation2를 취해서 word2를 만들어낼 수 있는가 없는가를 판단하는 것이니까요) operation1과 operation2를 진행하는 예를 다시 보면, 연산 후에 나타나는 특징이 있었습니다. 그것은 바로 연산 후의 문자열의 개수가 변하지 않는다는 점입니다.

 

 만약, word1와 word2의 문자열 길이가 다르다면, word1에 operation1과 2를 아무리 시행해도, 백만 번 천만 번 시행한다고 해도 절대 word2를 만들어 낼 수 없음을 의미합니다. 따라서 word1과 word2의 길이를 비교해서, 만약 다르면 false를 리턴하도록 코딩을 해야합니다. 

 

다른 알파벳을 가지고 있는 경우

 word1과 word2가 다음과 같이 주어져 있다고 해 보겠습니다.

 

word1 = "aabbbccc"

word2 = "aabbbddd"

 

 이 때, word1에다가 operation1과 2를 가해서, word2로 바꿀 수 있을까요? 절대 바꿀 수 없습니다. operation1과 2를 어떻게 조합해서 몇 백번, 몇 천번 시행한다고 하더라도 word1을 word2로 바꾸는 건 절대 불가능합니다. 그 이유는 무엇일까요?

 word2에는 d라는 알파벳이 포함이 되어 있는데, 이는 word1에 포함되어 있지 않은 알파벳 입니다. operation1과 2를 통해 없는 알파벳을 만들어 내는 것 자체가 불가능하기 때문에, 즉 word1에 존재하지 않는 알파벳인 d를 만들어 낼 수가 없기 때문입니다.

 

알파벳의 개수별로 짝이 이루어져야 합니다

 지금까지의 논리 전개로 보면, 정답은 다음 조건을 만족해야 합니다.

 

1. 주어진 두 문자열의 길이가 같다.

2. word2를 이루는 모든 알파벳은 word1에 존재하는 것이어야 한다

 

그러니까, operation1과 2를 통해서 서로간의 변환될 수 있는 문자열은 다음과 같은 형태입니다.

 

 

 그런데 이 조건을 만족한다고 해서 무조건 정답이 되는것일까요? 다음 조건까지 만족해야만 합니다.

close string을 만족하려면 충족해야 하는 조건

 

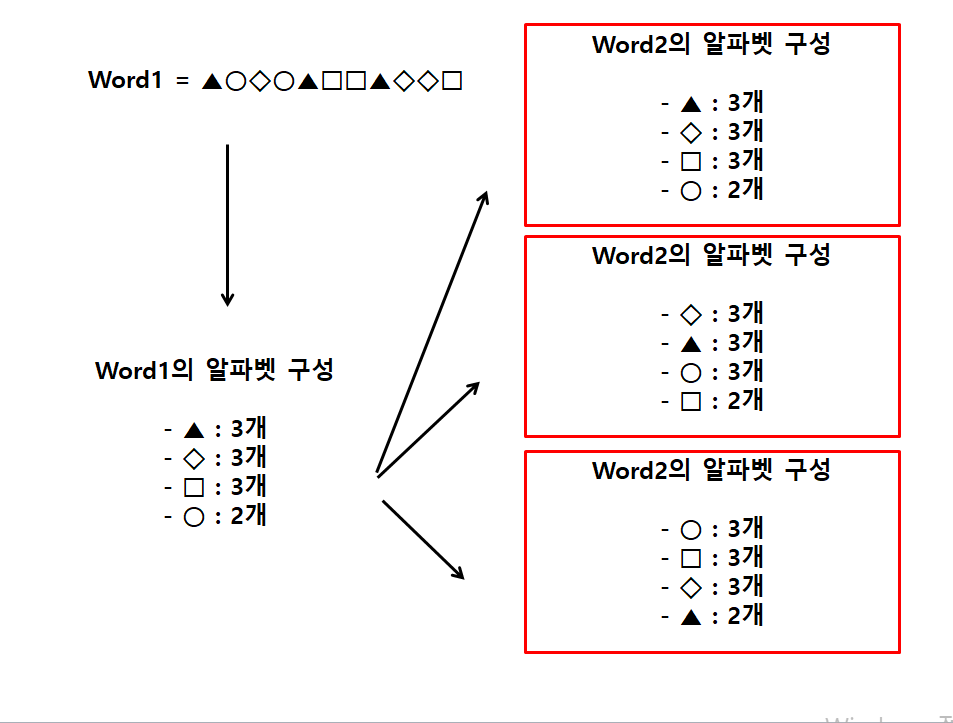
위 그림을 보면 word1은 세모 3개, 다이아몬드 3개, 네모 3개, 동그라미 2개로 이루어져 있습니다.

이 때, word1과 word2가 close string이기 위해서는

word2도 다음과 같은 형태로 구성되어 있어야 합니다. 

 

~ 알파벳 3개, ~ 알파벳 3개, ~ 알파벳 3개, ~ 알파벳 2개

 

예를 들면 다음과 같이 구성되어 있어야 한다는 의미입니다.

word1이 주어졌을 때, word2와 close string이기 위해서는 word2가 되어야 하는 형태

 

 

전체 소스코드

class Solution {
    public boolean closeStrings(String word1, String word2) {
        // 두 문자열의 길이가 다르다면 false 리턴
        if(word1.length() != word2.length())
            return false;

        // 각 문자열에서 알파벳의 개수를 세기 위한 배열
        int[] count1 = new int[26];
        int[] count2 = new int[26];

        for(char ch : word1.toCharArray())
            count1[ch - 'a']++;
        for(char ch : word2.toCharArray())
            count2[ch - 'a']++;       

        // word1에 존재하지 않는 알파벳이 word2에 존재한다면 false 반환
        for(int i=0; i<26; i++) {
            if(count1[i] == 0 && count2[i] != 0)
                return false;
        }

        // word1의 알파벳 별 개수와
        // word2의 알파벳 별 개수 쌍이 동일해야만 close string이다
        Arrays.sort(count1); Arrays.sort(count2);
        for(int i=0; i<26; i++) {
            if(count1[i] != count2[i])
                return false;
        }

        return true;
    }
}