URL : https://leetcode.com/problems/container-with-most-water/description/
LeetCode - The World's Leading Online Programming Learning Platform
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
오늘은 "가장 많은 물을 저장할 수 있는 컨테이너 찾기", LeetCode 11번 문제를 해결해보는 시간을 가지도록 하겠습니다. 긴 말 필요 없이, 문제부터 먼저 확인해 보도록 하겠습니다.
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]). Find two lines that together with the x-axis form a container, such that the container contains the most water.Return the maximum amount of water a container can store.
Notice that you may not slant the container.

Constraints:
- n == height.length
- 2 <= n <= 105
- 0 <= height[i] <= 104
문제 분석하기
문제에서 요구하는 것은 "가장 많은 물을 저장할 수 있는 컨테이너를 찾으라"는 것입니다. 문장만 봐서는 무얼 하라는 것인지 도무지 이해가 되지 않으니, 문제에서 들어준 예시를 이용해 설명하도록 하겠습니다.
문제에서 다음과 같은 정수 배열이 주어진다고 해 봅시다.
height = [1,8,6,2,5,4,8,3,7]
여기서 height의 각 원소의 의미는, "격벽의 높이"라고 볼 수 있습니다. 컨테이너를 이야기하고 있는데 갑자기 격벽이라니? 의아하실 수 있겠지만, 곧 격벽이 무엇인지, 컨테이너가 무엇인지 한번에 이해시켜 드리겠습니다. 즉, 위와 같이 주어진 경우, 다음과 같이 격벽이 설치되어 있는 것이라고 보시면 됩니다.

즉, 위 그림에서 보시는 바와 같이, height라는 배열의 각 인덱스의 높이에 해당하는 만큼 순서대로 배치된 모습이라고 볼 수가 있습니다. 우리는 이제 여기서, 두 격벽을 골라 물을 채울 예정입니다. 바로 다음과 같이 말입니다.

위 그림에서는 인덱스 1과 6에 해당하는 격벽을 골라 물을 채운 후의 모습을 나타내었습니다. 그러면 물이 위와 같이 고이게 되고 하나의 물을 담고 있는 단위가 생겨나게 되는 것입니다. 그리고 이 단위를 컨테이너(Container)라고 하는 것입니다. 따라서 다음과 같이 여러 경우의 컨테이너를 만들어 볼 수가 있을 것입니다.

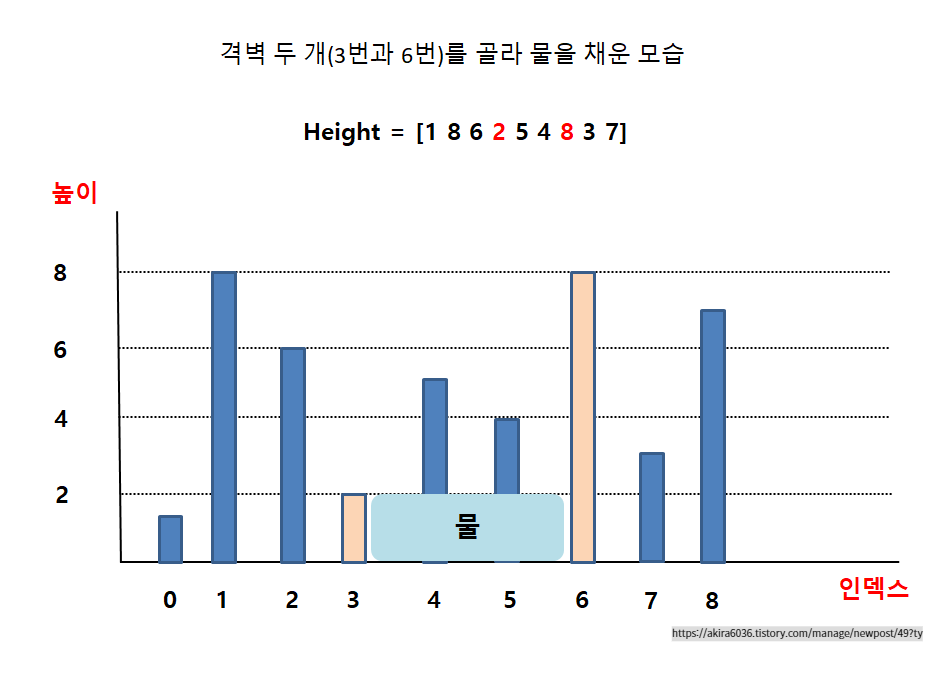
이렇게 0번 부터 8번까지의 격벽 중 두 개를 골라서 물을 부으면 위와 같이 "물이 담긴 컨테이너"가 생성되게 되는 것입니다. 문제에서 요구하는 것, '주어진 격벽 중에서 두 개를 골라, 가장 많은 물을 담을 수 있는 컨테이너를 만들라'는 것입니다. 그리고 그 컨테이너에서 물을 담을 수 있는 용량을 리턴하면 됩니다. 위의 예에서는 다음 컨테이너가 가장 많은 물을 저장할 수가 있습니다.

위와 같이 1번과 8번 인덱스의 격벽을 골라 컨테이너를 만들었을 때 가장 많은 물을 저장할 수가 있으며, 이 때 저장할 수 있는 물의 용량은 49(높이 7 X 밑면 7)입니다.
그러면, 위와 같이 격벽의 높이가 되는 배열(height)이 주어졌을 때에 위와 같이 최대 용량의 물을 저장할 수 있는 컨테이너를 어떻게 찾을 수 있는 지, 그 알고리즘을 공부해 보도록 하겠습니다.
느린 방법 : 브루트 포스(Brute Force) / 모든 경우의 컨테이너를 탐색하라!
가장 먼저, 모든 경우의 컨테이너를 구하고, 각 컨테이너의 물 저장 용량을 비교해, 가장 큰 값을 가지는 경우의 용량을 정답으로 리턴하는 방법이 있습니다.

예시에서 제공해준 경우를 한번 생각해 보겠습니다. 일단 만들 수 있는 모든 컨테이너를 구해야 합니다. 그리고 이렇게 구한 컨테이너들의 물 저장 용량들을 계산해야 합니다. 이렇게 계산된 물 저장 용량 중에서 가장 큰 값을 정답으로 리턴하면 문제가 해결됩니다.
컨테이너는 주어진 격벽들 중에서 두 개의 격벽을 선택해 형성되는 것이므로, 다음과 같은 경우들을 모두 비교해야 하겠네요.
경우 1. [0번 격벽 / 1번 격벽]을 골라 컨테이너를 구성하는 경우

경우 2. [0번 격벽 / 2번 격벽]을 골라 컨테이너를 구성하는 경우

경우 3. [0번 격벽 / 3번 격벽]을 골라 컨테이너를 구성하는 경우

... 너무 많아서 생략합니다...
경우 N-1. [6번 격벽 / 8번 격벽]을 골라 컨테이너를 구성하는 경우

경우 N. [7번 격벽 / 8번 격벽]을 골라 컨테이너를 구성하는 경우

그런데 이런식으로 문제를 풀면 풀리기야 하겠지만 문제가 있습니다. 그것은 바로.. 느리다는 것입니다. 데이터에서 주어진 격벽이 8개입니다. 컨테이너는 두 개의 격벽을 선택해 형성되므로, 다음과 같은 경우를 모두 고려하여 물을 최대한으로 저장할 수 있는 용량을 끄집어내야 합니다.
8C2 = (8)! / [(8-2)! x (2)!]
격벽이 n개라면, 다음과 같은 연산 / 비교횟수가 필요하며
nC2 = (n!) / [(n-2)! x (2)!] → "n에 대한 2차식"
문제 풀이에 소요되는 시간복잡도는 O(n^2)가 되는 것입니다.
따라서, 비 효율적인 풀이 말고(사실 무색해 보여도, 정석중의 정석이니 꼭 짚고 넘어가야 한다고 생각합니다),
시간복잡도 O(N)에 해결이 가능한 조금 더 효율적인 알고리즘을 공부해 보도록 하겠습니다.
빠른 방법 : 투 포인터(Two Pointer)를 이용하자
의아하실 수도 있을 것 같습니다. 글의 카테고리는 Greedy Algorithm인데 투 포인터라니. 알고리즘 문제라는 것에 카테고리가 주어져 있는 경우가 많습니다. 예를 들면 그리디 알고리즘 문제, 다이나믹 프로그래밍 문제 등등.. 그런데 그 알고리즘 문제를 풀어보면 딱 하나의 카테고리만 사용 되는 경우는 사실 잘 없고 여러 테크닉이 함께 사용되는 경우가 더 많습니다. 이 문제의 경우에는 투 포인터를 사용하면서. 동시에 그 성격이 그리디 알고리즘적 특징을 띄는 문제라고 보시면 됩니다.
투 포인터를 사용한 방법이 무엇인지 알아보기 전에, 어떤식으로 알고리즘이 동작하는 지 알아보도록 할겠습니다.
첫 번째로, 다음 그림과 같이 배열의 첫 지점을 왼쪽 포인터, 배열의 마지막 지점을 오른 쪽 포인터로 초기화합니다.
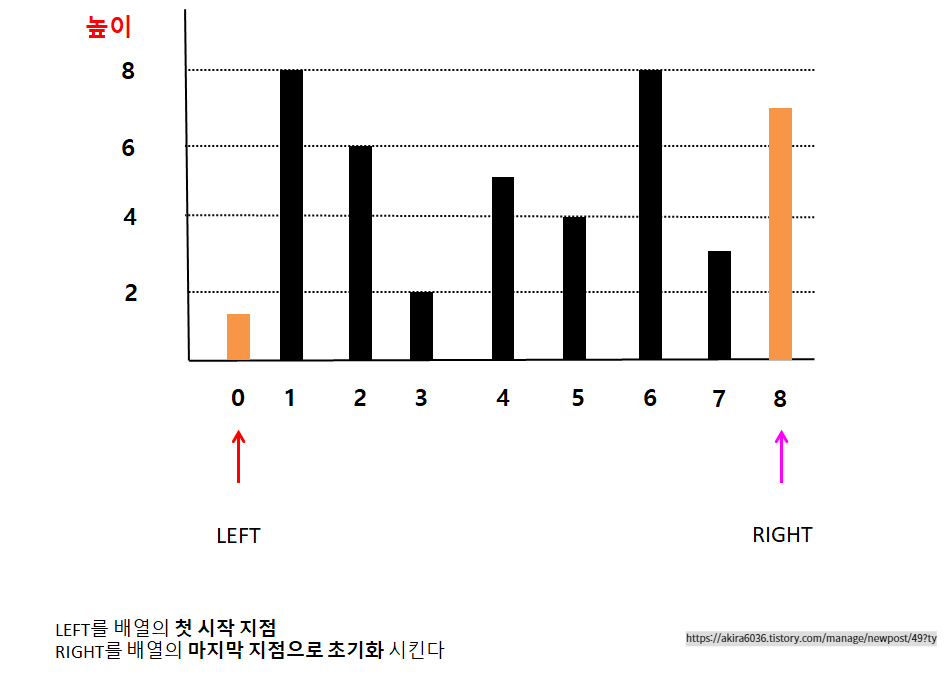
이제 이 왼쪽 포인터를 오른쪽으로 움직여 가면서,
오른 쪽 포인터를 왼쪽으로 움직여 가면서, 물을 최대한으로 저장할 수 있는 두 격벽을 고르는 작업을 할 것입니다. 이렇게 두 개의 포인터를 이용해 양 끝부터 차례대로 탐색하는 알고리즘을 투 포인터(Two Pointer) 알고리즘이라고 합니다. 그리고 왼쪽 포인터는 반드시 오른 쪽 으로만 이동을 하고, 오른 쪽 포인터는 왼 쪽으로만 이동을 시킬 것입니다.
매 단계마다, 투 포인터를 이용해 선택된 두 개의 격벽을 이용해서 얼마만큼의 물을 저장할 수 있는 지를 체크하기만 하면 됩니다.

그리고 다음 과정이 중요합니다!
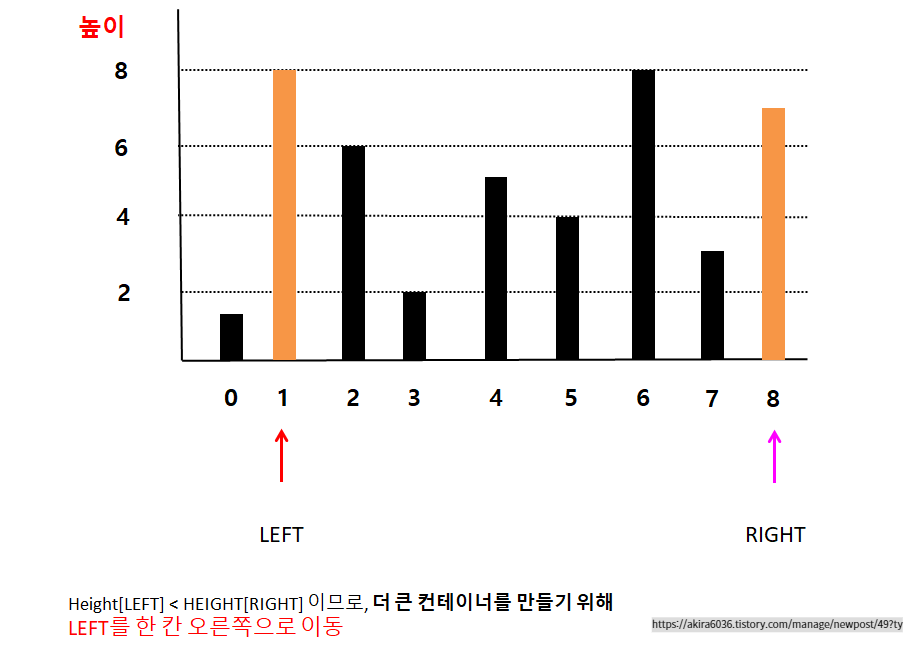
원래는 LEFT가 0번 격벽, RIGHT가 8번 격벽을 가리키고 있었습니다.
그리고 우리의 목표는, 방금 우리가 선택했던 두 격벽을 이용해 저장할 수 있는 물 저장 용량보다 더욱 많은 양의 물을 저장할 수 있는 두 격벽을 찾는 것입니다. 그러면 이 투 포인터를 어떠한 규칙으로 움직여야 할까요?
더 많은 양의 물을 저장할 수 있으려면 격벽의 높이가 높아야 합니다. 바꿔 말하면 더욱 높은 격벽을 선택할 경우, 더 많은 양의 물을 저장할 수 있습니다. 이 점에 착안하여, 왼쪽 포인터가 가리키고 있는 격벽의 높이, 오른쪽 포인터가 가리키고 있는 격벽의 높이를 비교합니다. 왼쪽 포인터가 가리키는 격벽의 높이가 오른쪽 포인터가 가리키는 격벽의 높이보다 크다면 오른쪽 포인터를 왼쪽으로 이동시키고, 오른쪽 포인터가 가리키는 격벽의 높이가 왼쪽 포인터가 가리키는 격벽의 높이보다 크다면 왼쪽 포인터를 오른쪽으로 이동시킵니다. 방금 볼드체로 표시한 문장, 가독성이 낮아 이해하기 어려우니 오글거리긴 하지만 다음 두 격벽의 대화를 통해 확인해볼까요?

투 포인터를 움직일 때마다 목표는 매 번 똑같습니다.
"더 많은 양의 물을 저장할 수 있는 경우를 찾고싶다!"
위 경우에서는, 왼쪽 포인터가 가리키는 격벽과, 오른쪽 포인터가 가리키는 격벽의 크기를 비교했을 때 오른쪽 격벽의 높이가 더욱 높습니다. 이 때 오른쪽 격벽을 왼쪽으로 이동시키면 어떻게 될까요? 그 어떠한 경우라도 더 많은 양의 물을 저장할 수 있는 경우를 찾을 수 없습니다. 물의 저장 용량은 이전 단계와 같거나, 최악의 경우 더 작아질 수가 있겠죠. 이러한 경우는 우리의 관심사가 아니라서 탐색을 진행하지 않습니다.
그래서 이러한 경우는 왼쪽 포인터를 오른 쪽으로 움직여야만, 더 많은 양의 물을 저장할 수 있는 경우를 찾을 수가 있는 것입니다. 이것이 바로 이 문제가 그리디(Greedy)알고리즘에 해당하는 이유입니다. 매 단계마다, 어떻게 하면 바로 다음 단계에 더욱 많은 양의 물을 저장할 수 있는 경우를 찾을 수 있을까를 고민하고, 그에 기반해서 투 포인터를 움직이기 때문이죠.

방금 언급한 규칙으로 투 포인터를 매 단계마다 이동시킨 후에, 물 저장용량을 측정하기만 하면 됩니다.

역시 투 포인터를 이동시킨 후,

저장 가능한 물 용량을 측정합니다.
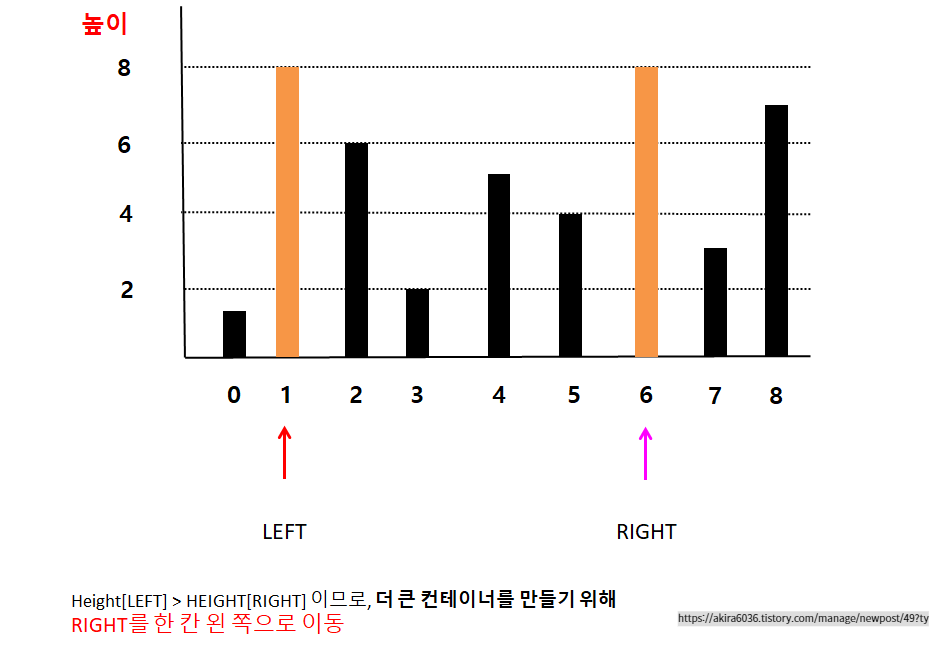
역시 동일한 규칙으로 투 포인터를 이동시킨 후,

저장 가능한 물의 용량을 측정합니다.

역시 동일한 규칙으로 투 포인터 이동 후 물 저장 용량 계산

역시 투 포인터 이동 후, 물 저장 용량 계산

이제 서서히 그림 그리기가 힘들어지기 시작합니다..

드디어 마지막이다.

투 포인터에서 LEFT를 오른쪽으로 이동시켜 가면서, RIGHT를 왼쪽으로 이동시켜 가면서 매 단계마다 두 포인터가 가리키는 물의 용량을 측정했었죠? 모든 단게에서 측정한 물의 용량중 가장 큰 값을 리턴하면 그게 정답이 됩니다! 그리고 위와 같이 투 포인터를 이동시켜 가면서 LEFT와 RIGHT가 겹치게 되는 순간이 옵니다. 그러면 반복문을 빠져나가고 정답을 리턴하면 되는 것입니다.
설명을 따라 오셨다면, 다음 소스코드를 보고 이해하실 수 있을 정도의 기반 실력이 갖추어 지셨습니다! 축하드립니다.
전체 소스 코드
class Solution {
public int maxArea(int[] height) {
// 물의 최대 저장 용량 갱신용 변수
int maxArea = -1;
// 왼쪽 포인터와 오른 쪽 포인터
int l = 0;
int r = height.length-1;
// 왼쪽 포인터와 오른 쪽 포인터가 겹치면 반복문 종료!
while(l < r) {
// 현재 두 포인터가 가리키는 격벽을 이용해 저장 가능한 물 용량 계산
// 최대 물 저장 용량 갱신
int area = (r - l) * Math.min(height[r], height[l]);
maxArea = Math.max(area, maxArea);
// 왼쪽 포인터가 가리키는 격벽의 높이 > 오른쪽 포인터가 가리키는 격벽의 높이라면
// 오른 쪽 포인터를 왼쪽으로 이동
if(height[l] > height[r])
r--;
// 반대의 경우면 반대로,
else
l++;
}
return maxArea;
}
}
마지막으로 설명을 드리자면, 현재 두 포인터가 가리키는 격벽이 저장할 수 있는 물의 용량을 계산하는 과정의 코드는 다음과 같습니다.
int area = (r - l) * Math.min(height[r], height[l]);
이게 왜 이렇게 나오는 지 그림으로 보여드리겠습니다^^

이 그림을 보시면 위 코드가 이해 되실 것이라고 생각합니다.
이상으로, LeetCode 11번 문제인 Containter With Most Water의 풀이를 마치겠습니다.
긴 포스팅 보시느라 수고 많으셨습니다.
감사합니다!